Комплексная автоматизация электростанции, также как и других энергетических установок, строится по иерархическому принципу, когда имеется несколько уровней контроля, защиты, регулирования и управления. Каждый уровень оснащается соответствующими средствами автоматизации и решает определенный круг задач.
Для транспортных судов рациональной представляется такая структура построения систем комплексной автоматизации (СКА), когда сочетается использование автоматических регуляторов и устройств, машин автоматического централизованного контроля (МАЦК), различных логических устройств, малых вычислительных машин и различного рода исполнительных элементов.
Такое распределение функций контроля, защиты, регулирования, управления и ответственности за результаты функционирования по уровням обеспечивает достаточную автономность уровней СКА и не перегружает высшие уровни большим объемом информации ограниченного характера.
Рис. 1. Структурная схема автоматизированной судовой электростанции: I - в цепь серводвигателя и схему запуска и остановки; II — отключение второстепенных потребителей
Кроме того, иерархический принцип построения СКА позволяет получить повышенную надежность и хорошие экономические характеристики, а также дает возможность вести поэтапное внедрение комплексной автоматизации, что особенно важно для уже действующих судов.
В настоящее время комплексная автоматизация интенсивно внедряется на судах мирового морского транспорта. Автоматизация электростанций судов ведется двумя путями: построение СКА с помощью унифицированных устройств и систем, таких, как УВР, УСГ-1П, УРЧН и др.; построение СКА на бесконтактных логических элементах.
На рис. 1 приведена блочная схема одного из вариантов автоматизации судовой электростанции. Данная схема обеспечивает: автоматический запуск и остановку резервного генератора в зависимости от загрузки электростанции, автоматическую синхронизацию, распределение активной нагрузки между параллельно работающими генераторами и отключение второстепенных потребителей.
Ввод в действие системы управления осуществляется оператором, который соответствующими переключателями устанавливает очередность включения генераторных агрегатов. Она периодически изменяется для обеспечения равномерного использования моторесурса первичных двигателей или в случае выхода из строя каких-либо генераторных агрегатов. Ключи синхронизации КС устанавливают в положение «Автоматическая синхронизация». Выбирают «базовый» генератор и переключателем П выключают его питание.
Допустим, что работает генератор Г1. При увеличении нагрузки до определенного значения срабатывает устройство включения резерва 1УВР-1П1, которое формирует сигнал на автоматический запуск резервного генератора, который автоматически запускается, выходит на номинальную частоту вращения и возбуждается до номинального напряжения. После этого автоматически вступает в действие устройство синхронизации УСГ-1П. По окончании процесса синхронизации начинает действовать устройство УРЧН, распределяющее активные мощности между параллельно работающими генераторами. В случае перегрузки любого генератора начинают автоматически действовать устройства УРГ, которые отключают (с выдержкой времени) ступени второстепенных потребителей. С уменьшением нагрузки до определенной величины устройства УВР формируют сигналы на отключение одного из генераторов.
Наиболее перспективными СКА судовых электростанций являются системы, построенные на бесконтактных логических элементах.
Теоретической основой построения современных СКА является один из разделов математической логики — алгебра логики, называемая также исчислением высказываний или алгеброй Буля.
Логические устройства, являющиеся основой СКА, описываются логическими функциями. Функции в алгебре логики обычно называют логическими или переключательными функциями, а их аргументы — высказываниями, входными переменными или сигналами.
Переключательные функции выражают зависимость выходных переменных некоторого логического устройства от входных переменных.
Функции и их аргументы являются двоичными переменными, принимающими одно из двух значений 0 или 1. Таким образом, переключательные функции — это двоичные функции двоичных переменных. Причем, цифры 0 и 1 не выражают здесь количественных соотношений, а являются символами, поэтому алгебра логики является не алгеброй чисел, а алгеброй состояний.
Использование двоичной системы счисления в алгебре логики объясняется тем, что логические схемы строятся на элементах, которые могут находиться в двух устойчивых состояниях: «включено» или «выключено», «да» или «нет» и т. д.
Двоичная система счисления так же, как и десятичная, является позиционной системой счисления, т. е. значение каждой цифры изменяется с изменением ее положения (позиции) в числовой последовательности, например в числе 212 первая цифра 2 означает сотни, а последняя — единицы.
Представить десятичное число А в виде двоичного означает — представить его в виде:
где аn, an-1,...,a1, a0 — цифры двоичного числа, равные 0 или 1.
Цифры двоичного числа можно определять последовательно, начиная с a0 и кончая аn, следующим образом:
а) делим заданное число А на 2, в результате получаем целую часть частного
и в остатке а0;
б) делим А1 на 2, в результате получим в частном
и в остатке а1 и т. д. Процесс деления продолжается до тех пор, пока не получим в частном 0, а в остатке 1. Первый остаток при делении а0 является наименьшей значащей цифрой (цифрой младшего разряда).
Например, дано десятичное число А = 37. После выполнения: последовательного деления на 2 будем получать соответственно в частном А1 = 18, А2 = 9, А3 = 4, А4 = 2, А5 = 1, А6 = 0 и в остатке a0 = 1, a1 = 0, a2 = 1, a3 = 0, a4 = 0, a5 = 1. В результате получим: 37(10)= 100101(2) (табл. 1).
Таблица 1. Двоичное представление некоторых десятичных чисел
Переключательные функции в зависимости от числа входных переменных делятся на функции одной, двух и многих переменных.
Они чаще всего задаются таблицей истинности (таблицей соответствия, таблицей состояния) или аналитическим выражением. В таблице истинности переключательная функция является полностью заданной, если указаны ее значения для всех наборов, значений входных переменных.
Набором называют различные возможные комбинации значений входных переменных. При одной входной переменной (n = 1) количество наборов равно двум N = 2 (0,1), при двух входных переменных (n = 2) — четырем N = 4 (00, 01, 10, 11), при трех входных переменных (n = 3) — восьми и т. д. Следовательно, количество наборов определяется выражением N = 2n.
Областью определения переключательных функций от n аргументов является совокупность 2n булевых наборов. Задавая то или иное конкретное значение функции для каждого из 2n наборов, можно тем самым задавать одну из возможных функций переменных, которых может быть: Р = 2N = 22n т. е. при одной входной переменной — Р = 4, при двух — Р = 16, при трех — Р = 256 и т. д.
В булевой алгебре, как и в обычной, применим принцип суперпозиции, т. е. подстановка переключательных функций вместо аргументов в другую функцию. Например, имея две переключательные функции от двух входных переменных Y1f1(X0, Х1) и Y2=f(X2, Х3) с помощью подстановки X0 = f2(X2, Х3) можно получить функцию от трех переменных Y=f[f2(X2, Х3), Х1]. Это дает возможность строить функции с большим числом переменных из функций с меньшим числом переменных. Поэтому в алгебре логики важную роль играют переключательные функции одной и двух переменных, из которых, используя принцип суперпозиции, можно построить переключательные функции от любого числа входных переменных.
Переключательные функции одной переменной — их может быть четыре:
- функция Y0 = 0 называется нулевой (всегда ложной) функцией и читается «Y0 есть 0»;
- функция Y1=X называется функцией повторения значений входной переменной и читается «Y1 есть Х»;
- функция Y3 = 1 называется единичной (всегда истинной) функцией и читается «Y3 есть 1».
Переключательные функции двух переменных — основные функции алгебры логики. Четырем наборам входных переменных соответствует шестнадцать (Р=16) возможных переключательных функций.
Таблица истинности (табл. 2) составлена так, что порядковый номер индекса при функции в десятичной системе счисления соответствует записи его в двоичной системе счисления на наборах входных переменных. Таблица истинности имеет ось симметрии между восьмой и девятой функциями.
Следовательно, первые восемь функций можно назвать прямыми, а остальные восемь — инверсными, так как
Таблица 2. Таблица истинности переключательных функций двух переменных
Общая характеристика переключательных функции двух переменных приведена в табл. 3. Из таблицы следует, что шесть функций уже встречались среди функций одной переменной.
Функции Y0 и Y15 являются соответственно нулевой и единичной функциями. Функции Y3 и Y5 являются функциями повторения и зависят каждая только от одной из двух переменных.
Функции Y10 и Y12 есть инверсии одной из входных переменных, т. е. фактически являются функциями только одной переменной. Остальные десять переключательных функций двух нерешенных являются оригинальными, поэтому рассмотрим их подробнее (нумерация — согласно номерам в табл. 3).
2. Конъюнкция (логическая операция И) в случае двух входных переменных записывается: Y1 = X0X1 читается "Y1 есть X0 и Х1". Как видно из табл. 2, функция принимает значение 1 только тогда, когда все ее входные переменные имеют значение 1. Во всех остальных случаях она принимает значение 0.
3 и 5. Запрет записывается: Y2=Х0Х1 при запрете по X1 или
при запрете по Х0. Функция принимает значение 0, если запрещающая входная переменная равна 1 при любом значении другой входной переменной.
7. Неэквивалентность записывается:
Функция принимает значение 1, когда входные переменные имеют разные значения.
8. Дизъюнкция (логическая операция ИЛИ) записывается: Y7= X0+X1, читается "Y7 есть Х0 или Х1". Функция принимает значение 1, если хотя бы одна входная переменная равна 1.
9. Антидизъюнкция (стрелка Пирса) записывается:
читается «Y8 есть инверсия дизъюнкции переменных X0, X0». Функция является инверсией дизъюнкции и принимает значение 1 только тогда, когда обе входные переменные равны 0.
10. Эквивалентность записывается:
Функция является инверсией неэквивалентности и принимает значение 1 тогда, когда обе входные переменные имеют одинаковые значения.
Таблица 3. Переключательные функции двух переменных
12 и 14. Импликация записывается:
при импликации от X1 к Х0 или
при импликации от Х0 к Х1. Функция является инверсией запрета и принимает значение 1 всегда, когда разрешающая (имплицирующая) входная переменная равна 1.
15. Антиконъюнкция (штрих Шеффера) записывается:
читается «Y14 есть инверсия конъюнкции переменных Х0 и X1». Функция является инверсией конъюнкции и принимает значение 0 только тогда, когда обе входные переменные равны 1.
Основные законы алгебры логики устанавливают эквивалентность логических формул. Они дают возможность записать ряд выражений, с помощью которых можно осуществлять эквивалентные преобразования сложных логических формул с целью приведения их к более простому и удобному в дальнейшем использовании виду.
Закон нулевого множества. Согласно этому закону конъюнкция любого числа переменных обращается в нуль, если хотя бы одна переменная имеет значение 0: X0X10X3...Xn-1=0.
Закон универсального множества. Дизъюнкция любого числа переменных обращается в единицу, если хотя бы одна переменная имеет значение 1: Х0 + X1 + Х2 + 1 + Х4 + ... + Xn-1 = 1.
Закон идемпотентности (тавтологии, повторения). Конъюнкция и дизъюнкция, состоящие из любого количества одной и той же переменной, равны самой переменной: ХХХ = Х; Х+Х+Х = Х.
Закон двойной инверсии. Двойная инверсия не изменяет сущности логического выражения, т. е. двойная инверсия равносильна ее отсутствию:
Закон логического противоречия. Конъюнкция переменной и ее инверсии есть всегда нуль:
Закон исключенного третьего. Дизъюнкция переменной и ее инверсии есть всегда единица:
Закон коммутативности (переместительный). Согласно этому закону переменные в случае дизъюнкции или конъюнкции можно менять местами: для дизъюнкции X0+X1 = X1+X0; для конъюнкции X0X1=X1X0.
Закон ассоциативности (сочетательный). Данный закон устанавливает: для дизъюнкции (X0 + X1) + X2 = Х0 + (Х1 + Х2); для конъюнкции (Х0Х1)Х2 = Х0(Х1Х2).
Дистрибутивные (распределительные) законы:
- первый дистрибутивный закон, согласно которому конъюнкция относительно дизъюнкции раскрывается, как и в обычной алгебре: Х0(Х1+Х2) =Х0Х1 + Х0Х2;
- второй дистрибутивный закон, специфичный закон алгебры логики, согласно которому дизъюнкция относительно конъюнкций раскрывается: Х0 + (X1X2) = (Х0 + Х1) (Х0 + Х2).
Закон инверсии (правила де Моргана). Закон инверсии для логического сложения устанавливает, что отрицание дизъюнкции двоичных переменных эквивалентно конъюнкции их отрицаний:
Закон инверсии для логического умножения устанавливает, что отрицание конъюнкции двоичных переменных эквивалентно дизъюнкции их отрицаний:
В алгебре логики важное место занимает принцип двойственности. Две переключательные функции называются: двойственными, если одна получается из другой заменой каждой операции конъюнкции на дизъюнкцию и наоборот.
Отличают двойственные формы функции от инверсных функций, которые получаются из исходных их инверсированием. При этом не только все операции заменяют на двойственные, но и все переменные заменяют их инверсиями.
Заметим, что все рассмотренные законы остаются: справедливыми при замене входных переменных любыми переключательными функциями.
Функционально полные системы элементарных переключательных функций используют при разработке судовых СКА, когда возникает необходимость в реализации сложных переключательных функций.
Система (набор) элементарных переключательных функций называется функционально полной, если любая переключательная функция может быть представлена в виде суперпозиции функций этой системы.
Понятие функциональной полноты относится и к логическим элементам. Набор логических элементов называется функционально полным, если только из этих элементов можно построить любую логическую схему. Наиболее употребительными полными наборами логических элементов являются: набор из логических элементов НЕ, И, ИЛИ; набор из одного универсального логического элемента ИЛИ—НЕ (стрелка Пирса); набор из одного универсального логического элемента И—НЕ (штрих Шеффера).
Из алгебраической записи переключательных функций двух переменных (см. табл. 3) видно, что для реализации любой из них вполне достаточно набора трех элементарных операций НЕ, ИЛИ, И. Функциональную полноту наборов ИЛИ—НЕ, И—НЕ можно доказать, показав, что только на одном из них можно получить все три операции НЕ, ИЛИ, И.
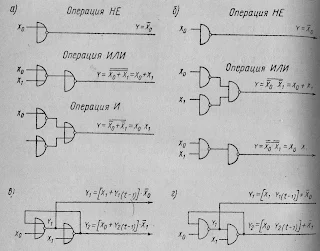
Используя известные выражения алгебры логики:
и логический элемент ИЛИ — НЕ, реализующий функцию
можно получить (рис. 2,а) все указанные логические операции. Этого же можно добиться (рис. 2,б) с помощью элемента И — НЕ, реализующего функцию
используя выражения:
Причем, операция НЕ получается, если в элементах ИЛИ — НЕ либо И — НЕ используется только один вход (или на все входы подается один и тот же сигнал).
Все логические устройства подразделяются на комбинационные (однотактные) и последовательностные (многотактные).
Комбинационными называются логические устройства, каждый выход которых зависит только от комбинации входных сигналов в данный момент времени (текущий такт).
Последовательностными называются логические устройства, выходные сигналы которых зависят не только от комбинации входных сигналов в текущий такт, но и от предшествующего состояния логического устройства, т. е. имеют элемент ПАМЯТЬ.
Рис. 2. Реализация логических операций НЕ, ИЛИ, И и элемента ПАМЯТЬ на элементах ИЛИ—НЕ, И—НЕ
Они в свою очередь, бывают синхронные (управляемые синхронизирующим источником — часами) и асинхронные.
В судовых СКА элемент ПАМЯТЬ реализуется на элементах ИЛИ — НЕ или И — НЕ. Он представляет собой схему (рис. 2, в, г), состоящую из двух соответствующих элементов, когда на один из входов каждого элемента подается выход другого элемента этой же схемы.
В схеме ПАМЯТЬ на элементах ИЛИ — НЕ (рис. 2, в) при подаче на вход Х0 сигнала, равного 1 (при X1 = 0), на одном выходе появится сигнал Y2 = 1, а на другом — инверсный по отношению к нему сигнал Y1 = 0. Если на вход Х1 подан сигнал 1 при Х0 = 0, то на выходах схемы ПАМЯТЬ появятся сигналы Y2 = 0, Y1 = 1. Это состояние сохранится (запомнится) и при изменении сигнала на входе X1 с 1 на 0. Схема ПАМЯТЬ ка элементах ИЛИ — НЕ может быть описана выражениями:
где Y1(t-1), Y2(t-1) — значения выходов в предшествующий такт.
В процессе анализа, эксплуатации и поиска неисправностей СКА судовых электростанций нужно уметь читать логические схемы и записывать реализуемые или переключательные функции.
Сложные логические схемы, как правило, разбиты на отдельные части (блоки). Определив все входы Xi и выходы Yi блоков, записывают переключательные функции, начиная от исполнительного элемента (выхода блока), и путем подстановки выходов предыдущих элементов на вход последующих (на основании принципа суперпозиции) движутся к входам блока.













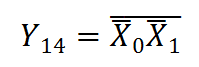













.JPG)


Комментариев нет:
Отправить комментарий