где J — момент инерции системы; ω — угловая скорость.
Если рабочая машина соединена непосредственно с электродвигателем, то под моментом инерции J подразумевается суммарный момент инерции ротора двигателя, соединительной муфты и вращающегося органа рабочей машины.
Если рабочая машина соединяется с электродвигателем посредством механических передач, причем угловая скорость рабочей машины отличается от угловой скорости ротора двигателя, то кинетическая энергия системы:
где Jn — момент инерции n-й ступени; k — число ступеней передачи.
При наличии у рабочей машины кроме вращающихся частей поступательно движущихся общая кинетическая энергия:
где l — число поступательно движущихся органов машины; mp — масса p-го поступательно движущегося органа; υp — его линейная скорость.
Для упрощения расчетов при исследовании движения подобного электропривода вводится понятие эквивалентного момента инерции, приведенного к валу электродвигателя.
Условием приведения является равенство кинетических энергий реальной системы и эквивалентного ротора электродвигателя, вращающегося с той же угловой скоростью:
Следовательно, эквивалентный момент инерции:
Учитывая, что jn = ωм/ωn — есть передаточное число от вала двигателя к n-му валу механизма, получают:
причем суммирование выполняют по всем вращающимся и движущимся частям.
Если вращающаяся система под действием внешних сил изменяет свое состояние, то возникает избыточная, или динамическая, мощность, вызванная изменением кинетической энергии:
и избыточный, или динамический, момент:
Используя выводы из начала Даламбера, можно записать условие равновесия моментов вращающейся системы, состоящей из двигателя и рабочей машины:
где Мд — момент на валу электродвигателя; Мс — статический момент рабочей машины, приведенный к валу двигателя.
Обычно на судах встречаются электроприводы, у которых момент инерции постоянен, в этом случае динамический момент определяется только вторым слагаемым:
тогда
или
Это уравнение называется основным уравнением теории электропривода.
Условием получения приведенного к валу двигателя статического момента сопротивления Мс является равенство мощностей приведенной системы и реальной:
где Мр.м — момент сопротивления на валу рабочей машины; ωр.м — угловая скорость вала рабочей машины; η — коэффициент полезного действия передачи.
Откуда
где j = ωм/ωр.м — передаточное число от вала рабочей машины к валу электродвигателя.
Анализ основного уравнения электропривода показывает, что при Мд >Мс ʃ (dωм/dt) > 0 угловая скорость системы увеличивается, а при Мд < Мс ʃ (dωм/dt) < 0 угловая скорость уменьшается.
Для нормальной работы системы двигатель — рабочая машина с постоянной угловой скоростью необходимо условие dωм/dt = 0 или Мд = Мс.
На рис. 1 приведены механические характеристики асинхронного двигателя 1 и рабочей машины первого класса 2. Из рисунка видно, что во время пуска Мд > Мс, поэтому двигатель начнет разгоняться до тех пор, пока избыточный момент больше нуля, т. е. до точки а.
Рис. 1. Механические характеристики совместной работы двигателя с механизмом
Следовательно, режиму работы системы с ω = const соответствует точка пересечения характеристик двигателя и рабочей машины. Если нагрузка рабочей машины будет больше М'с = const > Мc (характеристика 3), то, как видно из рисунка, двигатель не запустится.
Однако не всегда двигатель может работать устойчиво совместно с рабочей машиной.
Предположим, что двигатель работает в режиме, соответствующем точке с. Под влиянием случайных изменений параметров системы, возможно нарушение равенства моментов Мд и М'с, и если Мд будет меньше М'с, то двигатель начнет останавливаться, что приведет к дальнейшему увеличению разности Мс — Мд вплоть до полной его остановки.
При Мд > Мс угловая скорость начнет увеличиваться, а вместе с ней увеличиваться избыточный момент, который вызовет дальнейшее нарастание угловой скорости вплоть до значения, соответствующего точке b.
Подобный анализ показывает, что точка b соответствует устойчивому режиму работы электродвигателя с механизмом (также, как и точка а), а точка с — неустойчивому.





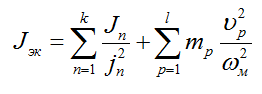



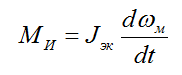









.JPG)


Комментариев нет:
Отправить комментарий